Survey of Rapid Training Methods for Neural Networks

Artificial neural networks are computing systems with interconnected layers that process and learn from data. During training, neural networks utilize optimization algorithms to iteratively refine their parameters until they converge to a solution that accurately models the data. This convergence process is crucial but can be extremely slow, taking days or weeks to complete with standard methods. Speeding up convergence enables quicker, more efficient neural network training; this allows these powerful models to be rapidly deployed for time-sensitive applications like self-driving cars, medical imaging, and fraud detection. Researchers have developed numerous innovative techniques to accelerate neural network convergence. This article compares popular methods of fast convergence methods for neural networks and provides insights into the most promising approaches for expedited training among the diverse options available.
Artificial neural networks have become indispensable for handling massive amounts of data across numerous domains. However, training these complex models can be time-consuming, sometimes taking days or weeks to converge to an optimal solution. This aspect restricts the usefulness of neural networks in real-world scenarios involving time constraints and limited computational resources.
Recently, researchers have developed innovative techniques to accelerate neural network training while maintaining or improving accuracy. In a new study, scientists extensively surveyed the latest methods for fast convergence in deep learning models. This work provides valuable insights into the most effective strategies for expediting neural network training.
The Trouble with Slow Training
The standard process for optimizing neural networks relies on iterative algorithms, which are algorithms that repetitively adjust the model’s parameters to minimize the value of a specified loss function. A loss function quantifies the disparity between the model’s predictions and the actual target values during the training process. Each iteration, often called an epoch, represents a complete pass through the entire training dataset. This iterative process gradually converges the model towards an optimal solution, allowing it to discern and capture robust features from the training data. However, the computational expenses and delays incurred during extensive training cycles pose challenges for time-sensitive applications.
For instance, autonomous vehicles must make split-second driving decisions based on real-time sensor data. Any lag in processing this data through a neural network model could lead to catastrophic outcomes. Similarly, fraud detection systems and medical diagnostic tools must rapidly analyze information and provide results within narrow time windows. Enhancing the convergence speed for neural networks is crucial to enable their deployment in such domains.
Beyond acceleration, faster training offers additional advantages like lowered power consumption, quicker model iteration, and the ability to handle larger datasets and more complex architectures. As high-performance computing (HPC) systems take on ever-more-ambitious applications in science and engineering, rapid training will become pivotal for realizing neural networks’ full potential.
Key Approaches for Faster Convergence
Six primary approaches have demonstrated enhanced convergence speeds during neural network training:
Weight Normalization: This technique restructures the model’s weights, which are the connections between nodes in the neural network, to transform them into a space better suited for optimization. By alleviating issues like vanishing gradients, where the gradient values become very small during backpropagation, making it difficult to train deeper networks, it streamlines training for both deep and recurrent neural networks.
Cyclical Learning Rates: Rather than using fixed or decreasing learning rates, which control the step size during training, this method adjusts them within a range, allowing periodic escapes from local minima. Local minima are suboptimal solutions in which algorithms can get stuck. The automated learning rate adaptation enables efficient exploration of the solution landscape, which refers to the relationship between the model parameters and the loss function.
Stochastic Gradient Descent (SGD): SGD approximates the true gradient, which indicates the direction of the steepest ascent, by sampling random mini-batches of data points. This approximation smooths and speeds up convergence for large datasets. Regularization methods like early stopping, which halts training when validation performance dips, and dropout, which randomly drops nodes during training, complement SGD to avoid instability.
Momentum Optimization: Momentum incorporates information from prior gradients to smooth out updates to model parameters. Damping oscillations, which are large fluctuations in parameter values, accelerate the traversal of flat regions in the optimization terrain, referring to the loss function landscape. Variants like Adam and Nesterov Accelerated Gradient (NAG) further enhance the convergence benefits.
Adaptive Learning: Algorithms like AdaDelta and Adamax automatically tune learning rates for each parameter based on gradient information, eliminating the tedious manual tuning of this hyperparameter. This adaptive strategy delivers faster and more precise convergence by customizing the learning process. Numerous adaptive gradient algorithms exist, including Adadelta, Adamax, Nadam (Adam and Nesterov’s momentum), AMSBound, Adabound, and Adagrad.
Natural Gradient Descent: Techniques like RMSprop, K-FAC, and Hessian-free optimization utilize second-order curvature data for more informed parameter updates. Despite added complexity, they achieve superior convergence and generalization.
Findings from Comparative Analysis
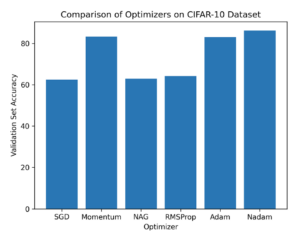
Researchers benchmarked implementations of the methods above on standard datasets like CIFAR-10 (a dataset contains 60,000 32×32 color images in 10 different classes) and ImageNet (an image database organized according to the WordNet hierarchy, in which hundreds and thousands of images depict each node of the hierarchy) to gauge performance. The key findings are as follows (see Figure 1)
- Weight normalization matched or exceeded the accuracy of other techniques, like batch normalization, while accelerating SGD convergence. Combining it with batch normalization yielded the best test accuracy overall.
- Cyclical learning rates consistently converged quicker across various models and datasets than fixed/decaying rates. However, determining optimal cycle lengths required extensive experimentation.
- Ensemble learning, which combines multiple models, substantially improved SGD’s convergence and generalization, which refers to the model’s ability to perform well on new unseen data. However, excessive dropout, where too many random nodes are dropped during training, impairs performance.
Adaptive algorithms like AMSBound and Nadam surpassed momentum methods and SGD in terms of speed and precision. But they required more memory and computations.
Natural gradient descent techniques achieved state-of-the-art convergence and accuracy. Yet, scaling them to huge datasets and models remained challenging due to their complexity.
In summary, the findings reveal that methods leveraging dynamic learning rates, adaptive parameter rescaling, and curvature data hold particular promise for expediting neural network training. However, factors like computational overhead, memory demands, and generalization capabilities necessitate careful selection of approaches based on the model architecture, dataset, and hardware constraints.
Future Outlook and Challenges
Current research highlights remarkable progress in fast convergence techniques, which will expand neural networks’ applicability to new domains. Nonetheless, several open challenges remain, such as developing adaptive methods that work across diverse network architectures and creating robust optimization algorithms tailored for specialized HPC environments.
Future work may also entail devising more holistic approaches that unite multiple promising techniques, such as cyclical learning rate schedules, ensemble training, and natural gradient optimization. Such unified frameworks could potentially achieve “super-convergence,” reducing training durations by an order of magnitude.
Enhancing neural network training efficiency with exponential data growth and model complexity remains imperative. Fast convergence methods are paving the way toward responsive, real-time artificial intelligence systems that leverage the full potential of HPC infrastructure. Continued research in this vibrant field will help overcome barriers to broader adoption across critical applications like healthcare, scientific computing, and smart infrastructure.
The graph in Figure 1 shows the comparative performance of different optimization algorithms. The performance evaluation is based on two criteria: convergence speed and test accuracy. The graph highlights that Nadam outperforms all other algorithms and achieves higher test accuracy than all other algorithms on CIFAR-10. The findings imply that Nadam is an extremely effective optimization algorithm for deep learning tasks. It delivers faster convergence and improved generalization compared to popular optimization algorithms like Adam and NAG.
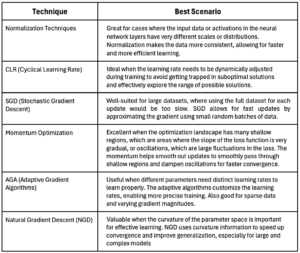
The following chart provides best practices for the various acceleration techniques mentioned above.
References for Further Investigation
[1] Salimans, T., & Kingma, D. P. (2016). Weight Normalization: A Simple Reparameterization to Accelerate Training of Deep Neural Networks. ArXiv. /abs/1602.07868
[2] Ioffe, S., & Szegedy, C. (2015). Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. ArXiv. /abs/1502.03167
[3] Ba, J. L., Kiros, J. R., & Hinton, G. E. (2016). Layer Normalization. ArXiv. /abs/1607.06450
[4] Ulyanov, D., Vedaldi, A., & Lempitsky, V. (2016). Instance Normalization: The Missing Ingredient for Fast Stylization. ArXiv. /abs/1607.08022
[5] Smith, L. N., & Topin, N. (2017). Super-Convergence: Very Fast Training of Neural Networks Using Large Learning Rates. ArXiv. /abs/1708.07120
[6] Smith, L. N. (2015). Cyclical Learning Rates for Training Neural Networks. ArXiv. /abs/1506.01186
[7] Hong Lin, Xiaodong Yang, Ruyan Xiong, and Binyan Wu. 2022. VTPC: Variable Trapezoidal Parity Cycle Learning Rate for Deep Neural Network. In 2021 International Conference on Mechanical, Aerospace and Automotive Engineering (CMAAE 2021). Association for Computing Machinery, New York, NY, USA, 222–228. https://doi.org/10.1145/3518781.3519183
[8] Park, S., Şimşekli, U., & Erdogdu, M. A. (2022). Generalization Bounds for Stochastic Gradient Descent via Localized $\varepsilon$-Covers. ArXiv. /abs/2209.08951
[9] Zhang, J., He, T., Sra, S., & Jadbabaie, A. (2019). Why gradient clipping accelerates training: A theoretical justification for adaptivity. ArXiv. /abs/1905.11881
[10] De, S., Mukherjee, A., & Ullah, E. (2018). Convergence guarantees for RMSProp and ADAM in non-convex optimization and an empirical comparison to Nesterov acceleration. ArXiv. /abs/1807.06766
[11] Loshchilov, I., & Hutter, F. (2017). Fixing Weight Decay Regularization in Adam. ArXiv. /abs/1711.05101
[12] Zeiler, M. D. (2012). ADADELTA: An Adaptive Learning Rate Method. ArXiv. /abs/1212.5701
[13] Kingma, D. P., & Ba, J. (2014). Adam: A Method for Stochastic Optimization. ArXiv. /abs/1412.6980
[14] George, T., Laurent, C., Bouthillier, X., Ballas, N., & Vincent, P. (2018). Fast Approximate Natural Gradient Descent in a Kronecker-factored Eigenbasis. ArXiv. /abs/1806.03884
[15] Kashyap, R. V. (2022). A survey of deep learning optimizers-first and second order methods. ArXiv. /abs/2211.15596